2025年高职单招《数学(中职)》每日一练试题02月17日
2025-02-17 15:50:12 来源:人人学历网
2025年高职单招《数学(中职)》每日一练试题02月17日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知向量a,b满足|a|=2,|bl=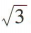 ,且a与b的夹角为30°,那么a·b=()
,且a与b的夹角为30°,那么a·b=()
- A:1
- B:
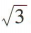
- C:3
- D:
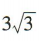
答 案:C
解 析: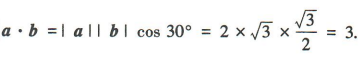
2、已知f(x)是R上的奇函数,当x>0时,f(x)=2x-1.若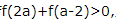 ,则a的取值范围是()
,则a的取值范围是()
- A:
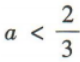
- B:
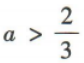
- C:
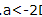
- D:
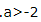
答 案:B
解 析:易知当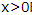 时f(x)=2x-1单调递增.因为f(x)是R上的奇函数,所以f(x)在(-∞,0)上单调递增,且f(0)=20-1=0.易知函数f(x)在R上单调递增.
时f(x)=2x-1单调递增.因为f(x)是R上的奇函数,所以f(x)在(-∞,0)上单调递增,且f(0)=20-1=0.易知函数f(x)在R上单调递增.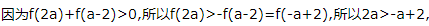 ,解得
,解得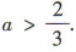
3、下列命题正确的是()
- A:终边相同的角是相等的角
- B:锐角是小于90°的角
- C:终边在第二象限的角是钝角
- D:相等的角终边重合
答 案:B
解 析:因为390°=30°+1×360°,所以390°角与30°角的终边相同,但是390°≠30°,故A错误;锐角是大于0°且小于90°的角,故B正确;-240°角的终边在第二象限,但-240°角不是钝角,故C错误;若两个角相等,但始边不同,显然它们的终边不相同,故D错误.
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知集合A={1.2.3},B={a,3.4}.若A∩B={2,3},则a=()
答 案:2
解 析:∵A∩B={2,3},所以2∈B,又B={a,3,4},∴a=2.
2、某高中学校三个年级共有学生2000名.若在全校学生中随机抽取一名学生,抽到高二年级女生的概率为 0.19,则高二年级的女生人数为()
答 案:380
解 析:易得高二年级的女生人数为2000x0.19=380.
3、两平行直线l1:3x+4y+2=0与l2:3x+4y-1=0之间的距离是()
答 案: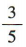
解 析:直线l1:3x+4y+2=0与l2:3x+4y-1=0之间的距离为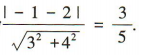
简答题
1、求k为何值时,二次函数f(x)=x2-(2k-1)x+(k-1)2的图像与x轴:(1)有2个不同的交点; (2)只有1个交点;(3)没有交点.
答 案:解:∵∆=[-(2k-1)]2-4(k-1)2 =4k2-4k+1-4k2+8k-4=4k-3 (1)当△>0时,有两个不同交点,4k-3>0,k>3/4 (2)当△=0时,只有一个交点,4k-3=0, k=3/4 (3)当△<0时,没有交点, 4k-3<0,k<3/



