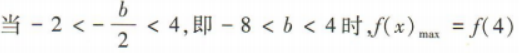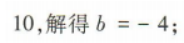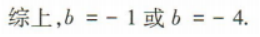2025年高职单招《数学(中职)》每日一练试题02月28日
2025-02-28 15:55:19 来源:人人学历网
2025年高职单招《数学(中职)》每日一练试题02月28日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知角α的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(2,-3),则cosα=()
- A:
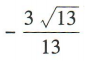
- B:
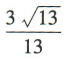
- C:
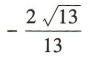
- D:
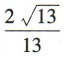
答 案:D
解 析:因为角α的终边经过点P(2,-3),所以P到原点0的距离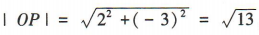 ,所以cosα=
,所以cosα=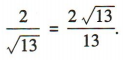
2、函数y=4sinx+3在[-π,π]上的单调递增区间为()
- A:
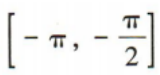
- B:
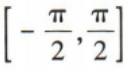
- C:
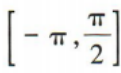
- D:
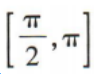
答 案:B
解 析:易知函数y=sinx的单调递增区间即函数y=4sinx+3的单调递增区间.因为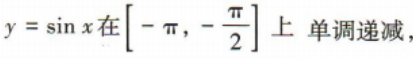
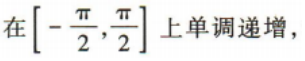
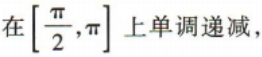

3、在幼儿园“体验分享,快乐成长”的活动中,有三位小朋友都把自己的一件玩具交给老师,老师再把这三件玩具随机发给他们,每人一件,则这三位小朋友都没有拿到自己玩具的概率是()
- A:
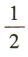
- B:
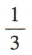
- C:
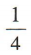
- D:
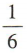
答 案:B
解 析:不妨设三位小朋友分别为A,B,C,且A的玩具为a,B的玩具为b,C的玩具为c,现将三个玩具随机分给三位小朋友,不同的情况有(a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a),共6种情况,其中三位小朋友都没有拿到自己的玩具的情况有(b,c,a),(c,a,b),共2种情况,所以所求概率为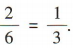
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、一个数分别加上20,50,100后得到的三个数成等比数列,则这个数为()
答 案:25
解 析:设所求的数为x.根据题意得(x+50)2=(x+20)(x+100),解得x=25.
2、若函数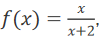 则
则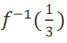 = _______
= _______
答 案:1
解 析:解法一:
由 得
得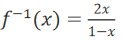 ∴
∴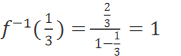 解法二:
由
解法二:
由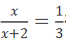 得x=1
∴
得x=1
∴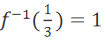
3、将钟表的分针拨快30分钟,则分针转过的弧度数是()
答 案:-π
解 析:将分针拨快30分钟,则分针顺时针旋转180°,所以分针转过的弧度数是-π
简答题
1、已知函数f(x)=x2+bx-2.
(1)若f(x)为偶函数,求不等式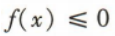 的解集;
(2)若f(x)在[-2,4]上的最大值为10,求b的值.
的解集;
(2)若f(x)在[-2,4]上的最大值为10,求b的值.
答 案:(1)因为f(x)为偶函数, 所以f(-x)=f(x),即(-x)²-bx-2=x²+bx-2,解得b=0,
所以f(x)=x²-2.