2025年成考专升本《高等数学一》每日一练试题05月24日
2025-05-24 11:26:04 来源：人人学历网
2025年成考专升本《高等数学一》每日一练试题05月24日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、设函数f（x）＝sinx，则不定积分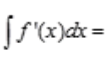
（）。
- A：sinx＋C
- B：cosx＋C
- C：-sinx＋C
- D：-cosx＋C
答 案：A
解 析：由不定积分性质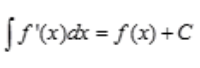
2、下列方程为一阶线性微分方程的是（）。
- A：
- B：
- C：
- D：
答 案：C
解 析：一阶线性微分方程的特点是方程中所含未知函数及其一阶导数都为一次的。因此选C。
3、
＝（）。
- A：3
- B：2
- C：1
- D：0
答 案：C
解 析：x2＋1在（-∞，∞）都是连续的，函数在连续区间的极限，可直接代入求得，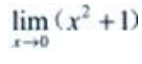
＝0＋1＝1。
主观题
1、试证：当x＞0时，有不等式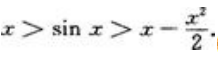
答 案：证：先证x＞sinx（x＞0）。设f（x）＝x－sinx，则f（x）＝1－cosx≥0（x＞0），所以f（x）为单调递增函数，于是对x＞0有f（x）＞f（0）＝0，即x－sinx＞0，亦即x＞sinx（x＞0）。再证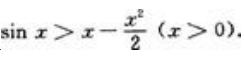
令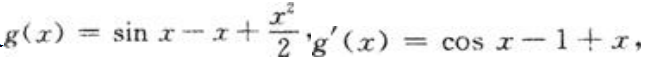
则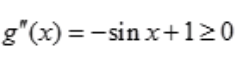
，所以g'(x)单调递增，又g'(x)＝0，可知g'(x)＞g'(0)＝0（x＞0），那么有g（x）单调递增，又g（0）＝0，可知g（x）＞g（0）＝0（x＞0），所以
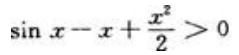即
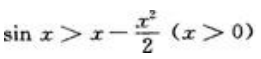
综上可得：当x＞0时，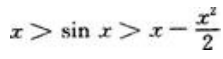
。
2、求y＝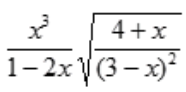
的一阶导数y'。
答 案：解：两边取对数得
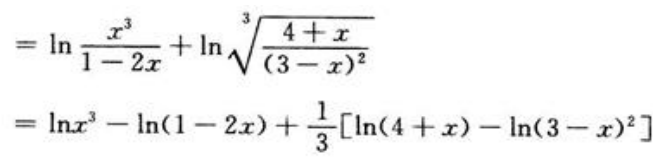两边对x求导得
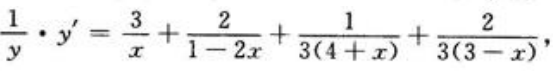故
3、求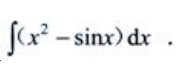
答 案：解：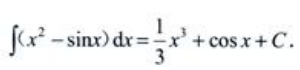
填空题
1、过点M0（1，-2，0）且与直线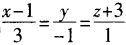
垂直的平面方程为（）。
答 案：3（x-1）-（y+2）+z=0（或3x-y+z=5）。
解 析：本题考查的知识点为平面与直线的方程。由题设条件可知应该利用点法式方程来确定所求平面方程。 
2、级数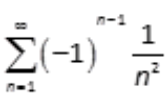
（）收敛。
答 案：绝对
解 析：因为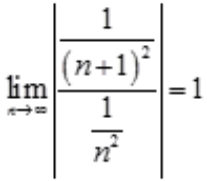
，又级数
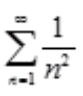收敛，所以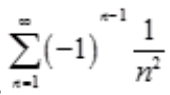
绝对收敛。
3、设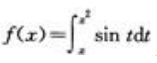
，则f'(x)＝（）。
答 案：2xsinx2-sinx
解 析：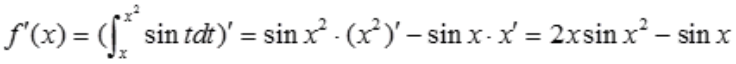
。
简答题
1、
答 案：
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
