2025年成考专升本《高等数学二》每日一练试题02月13日
2025-02-13 11:30:14 来源：人人学历网
2025年成考专升本《高等数学二》每日一练试题02月13日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、若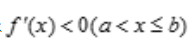
且f(b)＞0，则在（a，b）内必有（）.
- A：f(x)＞0
- B：f(x)＜0
- C：f(x)＝0
- D：f(x)符号不定
答 案：A
解 析：在（a，b），f'(x)＜0，f(x)单调减少，故f(x)＞f(b)，又f（b）＞0，所以f(x)＞0.
2、已知函数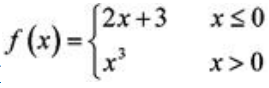
，则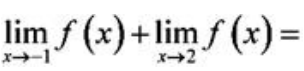
（）.
- A：9
- B：8
- C：7
- D：6
答 案：A
解 析：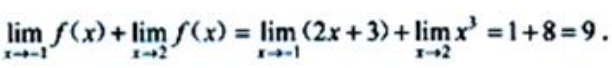
主观题
1、己知离散型随机变量X的概率分布为
（1）求常数a；
（2）求X的数学期望EX．
答 案：解：（1）因为0.2＋0.1＋0.5＋a＝1，所以a＝0.2．（2）EX＝10×0.2＋20×0.1＋30×0.5＋40×0.2＝27．
2、求函数f(x)＝x3－3x－2的单调区间和极值．
答 案：解：函数f(x)的定义域为（－∞，＋∞）．f'(x)＝3x2－3，令f'(x)＝0，得驻点x1＝-1，x2＝1．因此f(x)的单调增区间为（－∞，－1），（1，＋∞）；单调减区间为（－1，1）．f(x)的极大值为f(-1)＝0，极小值为f(1)＝－4．
填空题
1、二元函数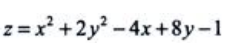
的驻点是（）
答 案：（2，-2）
解 析：
故驻点为（2，-2）
2、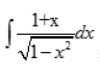
=（）
答 案：
解 析：
简答题
1、要做一个容积为V立方米的密闭圆柱形容器，两底面材料的价格为每平方米a元，侧面材料的价格为每平方米b元，问圆柱形容器的底面半径与高的比等于多少时，造价最低？
答 案：设底面半径和高分别为r，h，则造价函数L=2aπr2+2bπrh,且πr2，且πr2h=V 将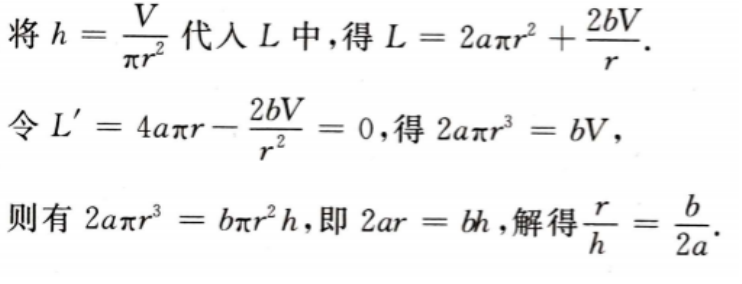
由实际问题的意义知，当底面半径与高的比为
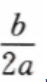时,造价最低.
2、求函数ƒ（x，y）=x2+y2在条件2x+3y=1下的极值
答 案：解设F（x，y，λ）=x2+y2+λ（2x+3y-1）， 
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
