2025年成考专升本《高等数学一》每日一练试题03月25日
2025-03-25 11:39:51 来源:人人学历网
2025年成考专升本《高等数学一》每日一练试题03月25日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、如果级数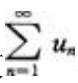 收敛,那么以下级数收敛的是()。
收敛,那么以下级数收敛的是()。
- A:
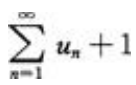
- B:
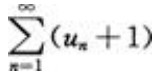
- C:
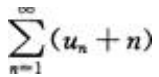
- D:
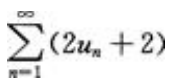
答 案:A
解 析:A项。级数 收敛,则
收敛,则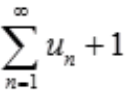 收敛;由极限收敛的必要条件可知,
收敛;由极限收敛的必要条件可知,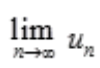 =0,则B项,
=0,则B项,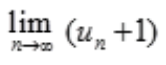 =1;C项,
=1;C项,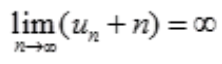 ;D项,
;D项,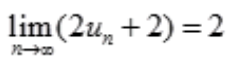 。
。
2、设f(x)在点x0处取得极值,则()。
- A:
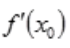 不存在或
不存在或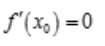
- B:
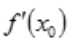 必定不存在
必定不存在 - C:
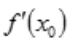 必定存在且
必定存在且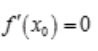
- D:
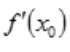 必定存在,不一定为零
必定存在,不一定为零
答 案:A
解 析:若点x0为f(x)的极值点,可能为两种情形之一:(1)若f(x)在点x0处可导,由极值的必要条件可知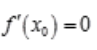 ;(2)如f(x)=|x|在点x=0处取得极小值,但f(x)=|x|在点x=0处不可导,这表明在极值点处,函数可能不可导。
;(2)如f(x)=|x|在点x=0处取得极小值,但f(x)=|x|在点x=0处不可导,这表明在极值点处,函数可能不可导。
3、设函数y=f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),曲线f(x)在(a,b)内平行于x轴的切线()。
- A:仅有一条
- B:至少有一条
- C:不存在
- D:不一定存在
答 案:B
解 析:由罗尔定理可知,至少存在一个 ,使得
,使得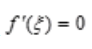 .而
.而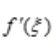 表示函数在
表示函数在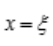 处的切线的斜率,所以曲线f(x)在(a,b)内平行于x轴的切线至少有一条。
处的切线的斜率,所以曲线f(x)在(a,b)内平行于x轴的切线至少有一条。
主观题
1、某厂要生产容积为V0的圆柱形罐头盒,问怎样设计才能使所用材料最省?
答 案:解:设圆柱形罐头盒的底圆半径为r,高为h,表面积为S,则 由②得
由②得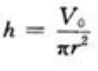 ,代入①得
,代入①得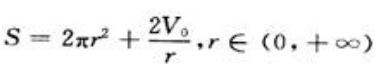
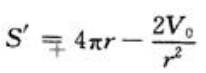 现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。
现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。
令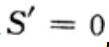 ,得
,得
由②,当 时,相应的h为:
时,相应的h为: 。
。
可见当所做罐头盒的高与底圆直径相等时,所用材料最省。
2、计算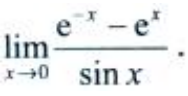
答 案:解:利用洛必达法则,得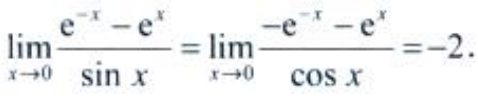
3、求
答 案:解: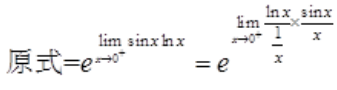
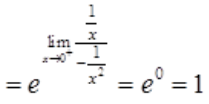 。
。
填空题
1、
答 案:1
解 析: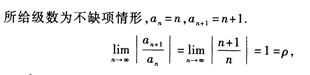
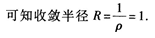
2、设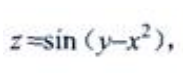 则
则 =()。
=()。
答 案: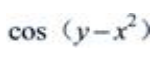
解 析: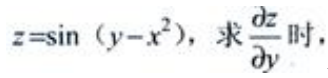 将x看作常量,则
将x看作常量,则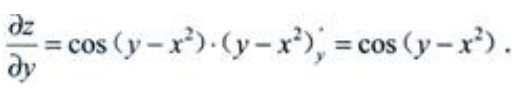
3、 =()。
=()。
答 案:e-1
解 析: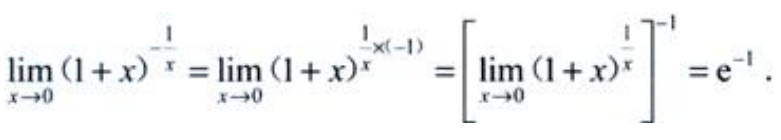
简答题
1、设F(x)为f(x)的一个原函数,且f(x)=xInx,求F(x)。
答 案:本题考查的知识点为两个:原函数的概念和分部积分法。 由题设可得知: