2025年高职单招《数学(中职)》每日一练试题02月15日

2025年高职单招《数学(中职)》每日一练试题02月15日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若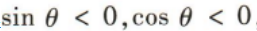则θ是（）

• A：第一象限角
• B：第二象限角
• C：第三象限角
• D：第四象限角

答 案：C

解 析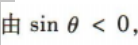： 得θ的终边在第三象限或第四象限或与y轴负半轴重合.由 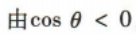得θ的终边在第二象限或第三象限或与x轴负半轴重合.所以θ是第三象限角.

2、过点 P(2,1)且斜率为1的直线方程是（）  

• A：x-y+1=0
• B：x-y-1=0
• C：x+y+3=0
• D：x+y-3=0

答 案：B

解 析：过点 P(2,1),且斜率为1的直线方程为y-1=1x(x-2),即x-y-1=0.

3、设a>b,a,b,c∈R,则下列结论正确的是()  

• A：ac²>bc²
• B：
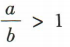
• C：a-c>b-c
• D：a²>b²

答 案：C

解 析：当c=0时，ac²=bc²,故A错误；当b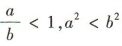22,，故B,D错误；因为a>b,所以a-c>b-c,故C正确.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、已知抛物线的方程为y²=8x,则抛物线的焦点到准线的距离是()  

答 案：4

解 析：因为抛物线的方程为y²=2px=8x,所以抛物线的焦点到准线的距离p=4.

2、满足M∪{1}={0.1.2}的集合M的个数为()  

答 案：2

解 析：因为M∪{1}={0,1,2},所以0,2必须是集合M中的元素，1可以是集合M中的元素，也可以不是集合M中的元素，所以M={0,2}或M={0,1,2},所以满足题意的M的个数是2.

3、圆x²+y²-2x=0的圆心到直线2x+y-1=0的距离为（）  

答 案：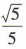

解 析：易知圆x²+y²-2x=0，即(x- 1)²+y²=1的圆心坐标为(1,0),则圆心(1,0)到直线2x+y-1=0的距离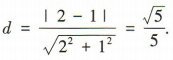

简答题

1、已知过点(2,0)的直线l与抛物线 C:y²= 4x 交于 A,B 两点. (1)若直线l的倾斜角为30°,求直线l与抛物线C准线的交点的坐标; (2)求弦长|AB|的最小值,并求出此时直线l的方程.  

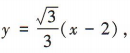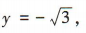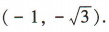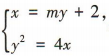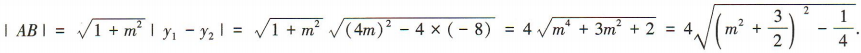答 案：(1)由抛物线的方程可得准线方程为x=-1. 由直线l的倾斜角为 30°且过点(2,0),得直线l的方程为 将x=-1代入上式得 所以直线l与抛物线C准线的交点的坐标为 (2)设A(x₁,y₁),B(x₂,y₂),直线l的方程为x= my + 2. 由得y²-4my-8=0, 则y₁+y₂= 4m,y₁y₂=-8, 所以 又m²≥0， 所以当m=0时,|AB|取得最小值,为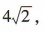 此时直线l的方程为x=2.