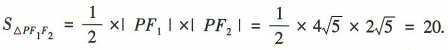2025年高职单招《数学(中职)》每日一练试题04月04日

2025年高职单招《数学(中职)》每日一练试题04月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知tanα=2,则()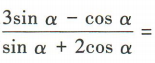  

• A：
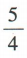
• B：
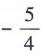
• C：
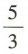
• D：

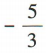
答 案：A

解 析：由tanα=2，得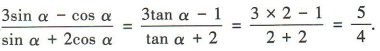

2、已知函数f(x)=x²-6x+8,x∈[1,a],且函数f(x)的最小值为f(a),则实数a的取值范围是（）

• A：(1,2)
• B：(1,3]
• C：(1,4]
• D：(1,5]

答 案：B

解 析：易得f(x)图像的对称轴为直线x=3.∵f(x)在[1,a]上的最小值为f(a),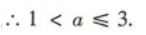

3、已知奇函数f(x)在区间[1,2]上的最小值为3,最大值为4,则f(x)在区间[-2,-1]上的()

• A：最小值为3,最大值为4
• B：最小值为-4,最大值为-3
• C：最小值为-3,最大值为4
• D：最小值为-4,最大值为3

答 案：B

解 析：由奇函数的图象关于原点对称及奇函数f(x)在区间[1,2]上的最小值为3,最大值为4,知f(x)在区间[-2,-1]上的最小值为-4,最大值为-3.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、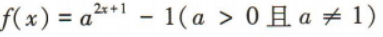的图像过定点（）

答 案：

解 析：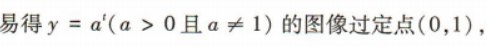

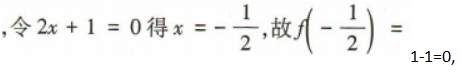
2、一个数分别加上20,50,100后得到的三个数成等比数列，则这个数为（）  

答 案：25

解 析：设所求的数为x.根据题意得(x+50)²=(x+20)(x+100),解得x=25.

3、某学校计划从5名女生,3名男生中选出4人参加数学竞赛,则选出的4人为2名女生和2名男生的选法有（）种.  

答 案：30

解 析：从5名女生,3名男生中选出2名女生和2名男生的不同选法有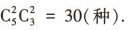

简答题

1、已知椭圆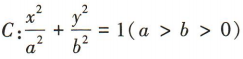的左、右焦点分别为F₁(-5,0),F₂(5,0),离心率为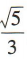,P为椭圆C上任意一点.(1)求椭圆C的标准方程;
(2)若，求 △PF₁F₂的面积.  

答 案：(1)由已知得c=5,,则 又b²=a²-c²=45-25 = 20, 所以椭圆C的标准方程为 (2)易知 因为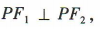 所以△PF₁F₂为直角三角形. 设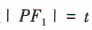,则,解得 所以或 所以