2025年高职单招《数学(中职)》每日一练试题05月18日
2025-05-18 15:51:00 来源:人人学历网
2025年高职单招《数学(中职)》每日一练试题05月18日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知点P(2m-1,m-1)在第一象限,则m的取值范围是()
- A:(1,+∞)
- B:(-1,+∞)
- C:(-∞,1)
- D:(-∞,-1)
答 案:A
解 析:
2、直线3x+4y-5=0与圆x2+y2=1的位置关系是()
- A:相交
- B:相切
- C:相离
- D:无法判断
答 案:B
解 析:易得圆x2+y2=1的圆心为(0,0),半径r=1,则圆心(0,0)到直线3x+4y-5=0的距离d=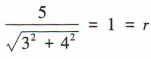 ,所以直线与圆相切.
,所以直线与圆相切.
3、已知函数f(x)=x2,那么f(x+1)=()
- A:x²+x+2
- B:x²+1
- C:x²+2x+2
- D:x²+2x+1
答 案:D
解 析:因为函数f(x)=x²,所以f(x+1)=(x+1)²=x²+2x+1.
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、设集合M={-1.0.1},B={0.1.2},则M∪B=()
答 案:{-1,0,1,2}
解 析:易知集合M={-1,0,1}和B={0,1,2}中的所有元素为-1,0,1,2,故M∪B={-1,0,1,2}.
2、若双曲线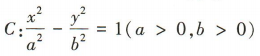 的虚轴长为8,渐近线方程为
的虚轴长为8,渐近线方程为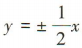 ,则双曲线C的方程为()
,则双曲线C的方程为()
答 案: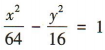
解 析:由题可得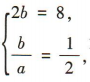 解得
解得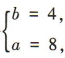 所以双曲线的方程为
所以双曲线的方程为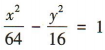
3、已知球的直径为2,则该球的体积是()
答 案: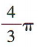
解 析:易得球的半径为1,故球的体积为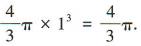
简答题
1、如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,且DC//AB,证明平面 PAB //平面 EFG.
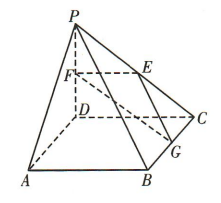
答 案:因为E,F分别是 PC,PD 的中点, 所以EF//DC.
又DC //AB,
所以 EF//AB.
又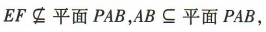 所以EF//平面PAB.
因为E,G分别是 PC,BC的中点,
所以 EG //PB.
又
所以EF//平面PAB.
因为E,G分别是 PC,BC的中点,
所以 EG //PB.
又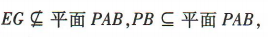 所以EG//平面PAB.
又
所以EG//平面PAB.
又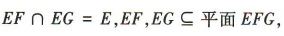 所以平面 PAB //平面EFG.
所以平面 PAB //平面EFG.



